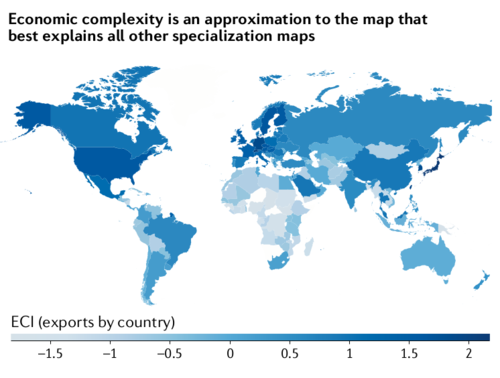
Economic complexity theory and applications
Complexity is a complex topic to define, as once it is defined well enough, can one still call it complex? In contrast to the definitions in my recent book review on complexity this is indeed how today's author describes complexity:
"In his paper “Science and complexity” 96 , the mathematician and AI pioneer Warren Weaver argued that science progressed as people discovered the mathematical languages needed to describe systems of increasing complexity."
There are two technical definitions which today's paper takes a deeper look into (1) relatedness and (2) complexity. A distinguishing aspect of the techniques that will be described below, is that the identity (the real measured values or characteristics of individual physical instances) are not ignored. Models are by definition a simplified representation of reality, but today's techniques try to stretch the amount of reality which can be fit into models.
Background
There are a couple of mathematical tricks that we will use in order to get a sense for relatedness and complexity. The first is the specialization matrix (if you are not familiar with Matrix notation, check out the tutorials here and here):
Xcp = volume of activity p in location c
"the volume of an activity may refer to exports, sales, total payroll, value added, employment or other quantities. Because matrices on the geography of activities include units of observation with sizes that are not readily comparable (for instance, China and Uruguay), they need to be normalized into specialization matrices."
As such a matrix may contain a wide range of values, a form of normalization is often desired. This can be done as follows:
Rcp = Xcp X / Xc Xp
Rcp is the ratio between the observed (Xcp ) and expected (XcXp/X) level of economic activity in a location. Locations with Rcp > 1 are considered to be specialized in activity p.
Let's look at an example, let's say that the following matrix represents total billions of dollars of revenue in the software (left column) and blogging (right column) industries, in the Netherlands (upper row) and the U.S. (lower row):
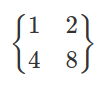
The normalized specialization matrix Rcp then clearly shows that the Netherlands is specialized in blogging, and the U.S. is specialized in software:
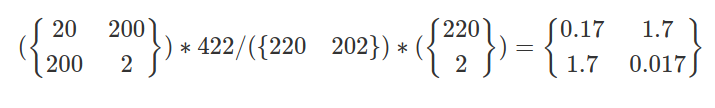
We can further highlight the differences by setting values to 0 and 1 at certain threshold. Summing the values of the columns will then give us a the level of ubiquity of each activity. Summing the values of the rows will give us the level of diversity for each location.
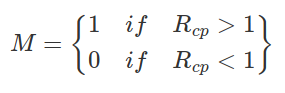
"A property of these geographic matrices is that the average ubiquity of the activities present in a location tends to correlate negatively with that location’s diversity. This fact is related to the matrix property known as nestedness and can be seen as evidence that more complex knowledge diffuses with more difficulty, and, hence, is only available at a few diverse locations."
Relatedness
You can predict a firm or region's ability to succeed in new economic activity by looking at how related their existing characteristics are, from geography to culture to technological proximity. The first measures of relatedness were relatively crude, focusing on the growth of locations specialized in bundles of related or unrelated activities. When a region only has completely identical activities or completely different activities, they score low on relatedness:
"Relatedness captures the intuition that learning requires interactions among activities that are similar, but not similar enough to be competing."
Which brings us to the principle of relatedness:
"the ‘principle of relatedness’ is a statistical law stating that the probability that a location enters or exits an activity is correlated with the presence of related activities."
Formally, relatedness ωcp can be defined as a predictor of a specialization matrix that satisfies:
Rcp(t + dt) = Rcp(t) + Bωcp(t) + ...
By looking at how different activities are correlated with each other, we can get a further understanding of which (pairs of) activities predict the increase or decrease in activity. A really cool extension of this model, is that relatedness can be "unpacked" into separate relatedness components so that you can for example observe the relative importance of industry-relatedness versus occupation-relatedness:
Rcp(t + dt) = Rcp(t) + B1ωcp1(t) + B2ωcp2(t) + ...
"Using data for the entire formal-sector economy of Brazil, (ref. 58) split relatedness into three channels: industry-specific, occupation-specific and location-specific relatedness. [...] Data on the birth of firms indicated that industry-specific relatedness, followed by location-specific relatedness, were the most relevant at explaining the entry, growth and survival of new firms. Surprisingly, occupation-specific relatedness did not matter for the entry of pioneer firms."
"Partialized measures of relatedness for technology, labour and supply chains have been used to reveal that relatedness-mediated entries are more likely to occur in upstream links (such as from assembly to parts) than in downstream links (from raw materials to products). This finding has important development implications, because it implies that diversification from raw materials to intermediate inputs tends to be a less frequent (probably less efficient) diversification path than diversification from final goods to intermediate inputs."
Complexity
Certain measurements of economic complexity have the ability to significantly and reliably predict economic growth. While in my previous articles on complexity, it was either seen as bad or neutral, here complexity is actually defined as something good, leading to positive outcomes.
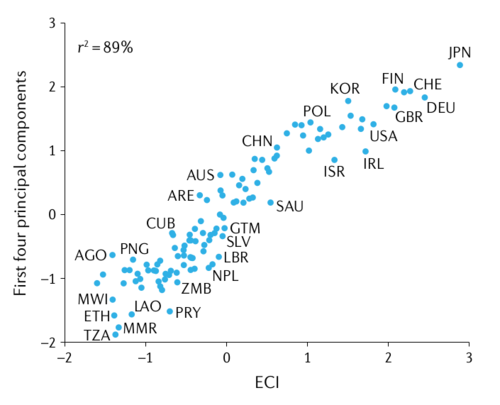
"Metrics of economic complexity measure the presence of multiple factors simultaneously, not by using aggregation (simplicity) or distributions (disorganized complexity) but by using dimensionality reduction techniques that preserve the identity of the elements involved and consider their interactions."
"Formally, the complexity Kc of location c and the complexity Kp of activity p can be defined as a function of each other. This means that they are solutions to a set of coupled equations"
Kc = f(Mcp , Kp)
Kp = g(Mcp, Kc)
"These general equations already eliminate important alternatives. For instance, they rule out metrics of market concentration, like those used in disorganized complexity approaches, such as the Shannon information entropy or the Herfindahl–Hirschman index (HHI). Metrics of diversity or concentration disregard information about the identity of elements involved by failing to couple locations and activities (for instance, HHI takes the form Kc = f(Mcp))."
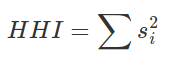
The Herfindahl–Hirschman measures is a measure of firm size and an indicator of the amount of competition. Here si is the market share of firm i in the market. This measure only takes into account activities within a location.
"The idea of measuring complexity using a set of coupled equations was introduced in 2009, using simple averages for f and g. The resulting metrics are known as the economic complexity index (ECI; Kc) and the product complexity index (PCI; Kp). [...] In economic terms, the ECI is the vector that is best at dividing economies into groups based on the activities that are present in them. [...] Economic complexity is intimately connected to singular value decomposition, a matrix factorization technique that provides the best way to explain the structure of a matrix."
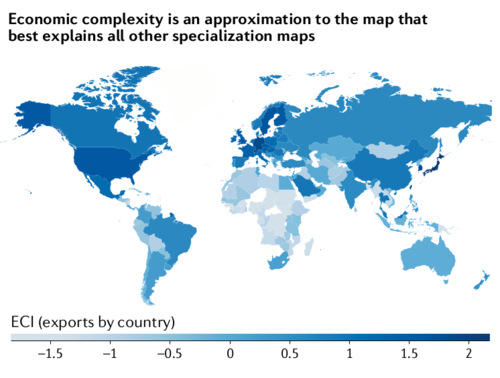
Economic complexity also seems to correlate positively or negatively with other factors like income inequality and sustainability measures, though these findings seem to me to be more nuanced and less extensively researched compared to the aforementioned findings on economic growth.
Common misconceptions
So when you want to drop fun facts about economic complexity during a dinner party, what are you actually allowed to say? Or, just as importantly for maintaining your social status, how can you nuance other people's arguments?
"One misconception is to equate economic complexity to measures of export diversity or concentration. This is wrong on two accounts. First, economic complexity, as measured by the ECI, is orthogonal — or nearly orthogonal — to measures of diversity or concentration. [...] Second, economic complexity is not about exports or trade (the use of trade data is convenient but not essential). It is a dimensionality reduction technique that summarizes the vectors that best explain the geography of thousands of economic activities."
Furthermore, the effectiveness of any empirical analysis is only as good as the data which can be collected - which can be pretty darn difficult when collecting data spanning multiple countries.
Finally, correlation is not causation, and although many economic complexity analyses use advanced statistical techniques and aim to control for lots of factors, you should be wary from drawing too many conclusions without remembering the situation where the analysis was done.
Policy implications
So, should we aim to maximize certain relatedness and complexity metrics because they correlate with things we like (economic growth, specialization)? Well empirical findings are mixed, but the theory prescribes the following:
"When applied to activities that are not present in a location, activities that are high in both relatedness and complexity represent the best ‘low-hanging fruit’ for diversification."
Reality is a bit more... complex:
"Mathematical models and numerical simulations have shown that always targeting high-relatedness activities is a suboptimal way to maximize diversification. Instead, economies should adapt their strategies by targeting relatively unrelated but connected activities during a window of opportunity that opens at intermediate levels of development."
Ultimately, the tools and formula's of economic complexity thrive on lots of good data. These tools are able to use a wide range of data to predict relatedness and complexity, including online repositories of collaborative work, such as GitHub, LinkedIn or IMDb. That kind of data is "naturally" created by economies, and not by economists, and therefore quite promising!
