2-dimensional Prisoner's Dilemma

In today's review, I will dive into an extension of a classic game which is the cornerstone of modern economics. Many of us may have learned this one already in high school: the Prisoner's Dilemma. As a quick refresher:
The game is played by pairs of agents, who simultaneously decide to either cooperate (C) or defect (D), receiving a payoff associated with their pairwise interaction as follows: R for mutual cooperation, P for mutual defection, S for cooperating with a defector and T for successfully defecting a cooperator. The dilemma holds when T > R > P > S.
The four different outcomes of the simple game can be visualized in the following payoff matrix:
| Player 1 cooperates | Player 1 defects | |
|---|---|---|
| Player 2 cooperates | (R, R) | (S, T) |
| Player 2 defects | (T, S) | (P, P) |
This shows for example that when Player 1 defects and Player 2 cooperates, player 1 gets reward T and player 2 gets reward S.
Whether you end up in a prison, fight or do a political formation, this matrix can help you choose between cooperating or defecting with others. This game is called a dilemma because, in case the players can't communicate with each other and the payoffs really measure the total benefit or utility a player receives, mutual defection is the optimal decision because T > R and the players have an incentive to defect. Mutual defection is called a Nash Equilibrium as it is the rational (but not necessarily optimal) decision.
Fortunately, reality doesn't always look like this. Today's article extends this basic model in the following ways. Today's model is:
- evolutionary, also known as iterated, which means that the game is repeated. Players take the results achieved by other players in the previous game into account to decide on their next action. If cooperation proved gave a high reward to some players, then this strategy is copied. A distinction can be made between games with synchronous updating (where players immediately copy the best strategy from their four neighbors) and asynchronous updating (where players randomly copy the best strategy from a single neighbor).
- spatial, which means that players are operating on a 2-dimensional grid, being able to play games with their direct neighbors to the north, east, south and west. In the current model, agents stay on their place, and therefore play four games against the same agents in each repetition before they re-calibrate their beliefs.
- using probabilistic abstention, as agents have a probability assigned to them between 0 and 1 which indicates the likelihood to abstain from even playing the game. But the joke is on them, they can never escape the game. Even if they abstain, they are simply assigned a different payoff L is added, which adheres to: T > R > L > P > S. such extensions are called optional prisoner’s dilemma. Abstention creates new interactions:
Studies reveal that the concept of abstaining can lead to entirely different outcomes and eventually help cooperators to avoid exploitation from defectors.
When abstention is present but only occurring with probability αi this creates the following payoff matrix:
| Player 1 cooperates | Player 1 defects | Player 1 abstains | |
|---|---|---|---|
| Player 2 cooperates | (R, R) | (S, T) | (α2L, α1L) |
| Player 2 defects | (T, S) | (P, P) | (α2L, α1L) |
| Player 2 abstains | (α2L, α1L) | (α2L, α1L) | (α2L, α1L) |
Findings and results
So in this environment, which strategies emerge?
it is possible to observe that the Prisoner's Dilemma with Probabilistic Abstention (PDPA) sustains higher levels of cooperation even for large values of the temptation to defect T. [...] In general, it is clear that irrespective of the updating rule, the PDPA game is most beneficial for the evolution of cooperation. Moreover, when comparing the Optional Prisoner's Dilemma (OPD) with the PDPA game, we see a correlation between their levels of abstention, showing that abstention may act as an important mechanism to maintain cooperation and avoid defector’s dominance.
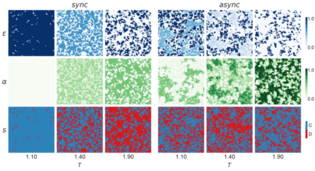
Given the nature of the classic PD and OPD games, it is known that in a well-mixed population, defection and abstention are usually the dominant strategies respectively. As discussed in previous work [22, 63], this happens because cooperators need to form clusters to be able to protect themselves against exploitation from defectors, and if we consider a randomly initialized population, it takes a few steps for cooperators to cluster.
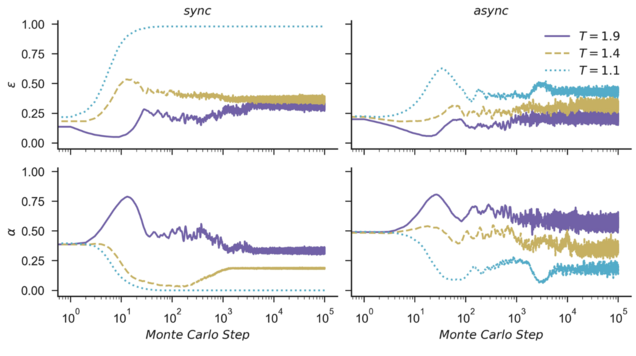
For the analysis the Monte Carlo method is used to run a large set of repeated experiments. The simulations are run using Evoplex: an agent-based modeling platform for networks, which aims at being a fast and modern (alright, it is built on C++14, so it is not thát modern) alternative to other simulation tools.
The following heat map illustrates the existence of "cooperation clusters" which emerge after some time of playing the game:
Where can we recognize these dilemma's?
The simple single-shot Prisoner's Dilemma explained above paints a bleak picture of humanity: there are situations where rational decisions can lead to disastrous outcomes through mutual defection. So why do the results of today's paper suggest that there are many situations where a solid amount of cooperation remains?
The following article does an excellent job at explaining:

Given that most Prisoner's Dilemmas in real life are actually iterated, realistic scenario's have huge action spaces (I can say X, go to location Y, but only if the other player bought good Z, etc. etc.) and complicated payoff matrices. In such an environment, there may be many different Nash Equilibria with different payoffs for the different players in the game. One equilibrium might be very beneficial for player 1, whilst another one may be more beneficial for player 2. If the players fail to coordinate towards one of the better equilibria, they might end up defecting to a worse equilibrium. This can happen for many reasons, from difficulty to identify payoffs, to failures to communicate, to plain irrationality and bias.
In a rational world with perfect information, many if not all equilibria can theoretically be enforced by the players on long term time frames, as the players can nudge and threaten their partners in the preferred direction. This looks a lot more like reality: we are negotiating with various groups of people in a complex environment towards a variety of equilibria. To make the most out of such an environment, remember:
Try to keep a path open toward better solutions [...] Keeping a path open for improvements is hard, partly because it can create exploitability. But it keeps us from getting stuck in a poor equilibrium.
Game theory for policymakers
Many articles and books note that the Prisoner's Dilemma was originally used to model the actions of the U.S. and Russia during the cold war. I personally doubt how much time government officials really spent calculating payoffs on a whiteboard. Perhaps one day, I will face an opportunity which allows me to draw a giant payoff matrix and exclaim: "Oh no! If there is an above 20% of abstention, then if I continue to cooperate, there is an above 60% chance that we can both live harmoniously together!" Instead, most decision's look more like how Darwin decided to marry: make a pro con list.
Are there situations where Game Theory can be directly used for decisionmaking? Perhaps there is an opportunity for policymakers; which already often make use of explicit models when taking decisions influencing large parts about society. These people are trained and get paid to shut up and multiply, hoping that models lead to a better outcome than operating just on intuition.
Unfortunately, the temptation to take a shortcut remains and policymakers may optimize for the wrong thing. A case study from the Netherlands is illuminating: party programs always provide excellent benefits for households with a median income, at the expense of households which do not fit neatly in one of the popular statistical boxes. Similarly, when modeling a situation with game theory, you risk being biased when picking payoffs or actions to include in your model as well. I hope citizens take that into account in their own payoff matrices!

